基于石墨烯的高質量二維電子系統已成為研究超導性的高度可調平臺。具體來說,在電子和空穴摻雜的扭曲石墨烯摩爾體系中都觀察到了超導現象,而在晶體石墨烯體系中,迄今為止只在空穴摻雜的斜方三層石墨烯(RTG)和空穴摻雜的Bernal雙層石墨烯(BBG)中觀察到了超導現象。最近,由于靠近單層 WSe
2,BBG 的超導性得到了增強。在此,報告了通過靜電摻雜在電子和空穴摻雜的 BBG/WSe
2 器件中觀察到的超導性和一系列味道對稱性破壞相。觀察到的超導電性的強度可通過施加垂直電場進行調節。電子摻雜和空穴摻雜超導的最大別列津斯基-科斯特利茲-無窮大轉變溫度分別約為 210 mK 和 400 mK。只有當外加電場將 BBG 電子或空穴波函數驅向 WSe
2 層時,超導性才會出現,這突出了 WSe
2 層在觀測到的超導性中的重要性。摻雜空穴的超導違反了保利順磁極限,與類伊辛超導體一致。相比之下,電子摻雜的超導電性遵守了保利極限,盡管在導帶中也有顯著的近似伊辛自旋軌道耦合。本研究的發現凸顯了 BBG 中與傳導帶相關的豐富物理現象,為進一步研究晶體石墨烯的超導機制和開發基于 BBG 的超導體設備鋪平了道路。

圖1. BBG/WSe
2的相圖及電子和空穴摻雜的超導性。a. BBG/WSe
2 雙柵器件示意圖。 b. D = 0 V nm
-1 時單層 WSe
2 和 BBG 的帶排列示意圖。BBG 的電荷中性點位于 WSe
2 半導體帶隙深處。c. 層間電位差 U = ±100 meV(大致相當于位移場 D≈ ±1 V nm
-1)時布里淵區 K 點和 K′點附近的單粒子帶結構計算結果。在正 D 時,空穴波函數集中在 BBG 的頂層,因此 WSe
2- 引發的 SOC 在價帶中更為突出。在負 D 時,電子波函數集中在 BBG 的頂層,因此 WSe
2-誘導的 SOC 在導帶中更為突出。 d. 在 T = 20 mK 時測量的 Rxx-D-n 圖,涵蓋了電子摻雜(0 < n < 1.0 × 10
12 cm
-2, -1.65 V nm
-1 < D < 1.60 V nm
-1)和空穴摻雜(-1.5 × 10
12 cm
-2 < n < 0, -1.55 V nm
-1 < D < 1.55 V nm
-1)區域。e. 根據 d 和量子振蕩的 FFT 分析確定的實驗相圖。我們使用 d 中的 R
xx 特征作為相界。假定自旋軌道耦合不混合,通過對量子振蕩的 FFT 分析,推斷出每個相位可能的費米面結構(如示意圖所示)。(f)i,不同 D 時空穴(f)和電子摻雜超導(i)的 dV
xx/dI
d.c. 與 I
d.c. 的關系。g,h,j,k,空穴超導(g)和電子摻雜超導(j)的 I
c(上)和 T
c(下)與 D 的關系,以及摻空穴一側在 D = 1.1 V nm
-1 時(h)和摻電子一側在 D = -1.64 V nm
-1 時(k)的 R
xx 與 n 的溫度關系。插圖顯示了最佳摻雜狀態下 R
xx 與 T 的關系曲線,此時 T
c 達到最高值。

圖2. 摻孔超導的費米面分析。a,b,D = 1.1 V nm
-1 (a) 和 1.5 V nm
-1 (b) 時摻雜空穴一側的 Rxx 與 n 和 B
⊥ 的關系。c,d,D = 1.1 V nm
-1 (c) 和 1.5 V nm
-1 (d) 時摻雜空穴一側的 R
xx (1/B
⊥) 與 n 和 f
ν 的 FFT 關系。c 和 d 中的 FFT 分析分別基于 0.2 T < B
⊥ < 1 T 范圍內的 R
xx 數據。不同相位的費米面結構示意圖也顯示在 c 和 d 中。不同相位的 FFT 頻率峰值用紅色箭頭標出。在 D = 1.1 V nm
-1 時,在 PIP
2 相內靠近三方翹曲相的位置觀察到一個超導區 (SC),該超導區由 Ising SOC 誘導的自旋分裂形成。

圖3. 電子摻雜超導電性的費米表面分析。a,b,D = 1.55 V nm
-1 (a) 和 -1.55 V nm
-1 (b) 時電子摻雜側的 R
xx 與 n 和 B
⊥ 的關系。c,d,D = 1.55 V nm
-1 (c) 和 -1.55 V nm
-1 (d) 時電子摻雜側的 R
xx (1/B
⊥) 與 n 和 f
ν 的 FFT 關系。c 和 d 中的 FFT 分析分別基于 a 和 b 中 0.2 T < B
⊥ < 1 T 范圍內的 R
xx 數據。c 和 d 中還顯示了不同相的費米面結構示意圖。e, f,摻電子一側在 B = 0 T、D = 1.55 V nm
-1 時(e)和-1.55 V nm
-1 時(f)的 R
xx 與 n 的關系。只有在負 D 時才能觀察到電子摻雜超導現象。
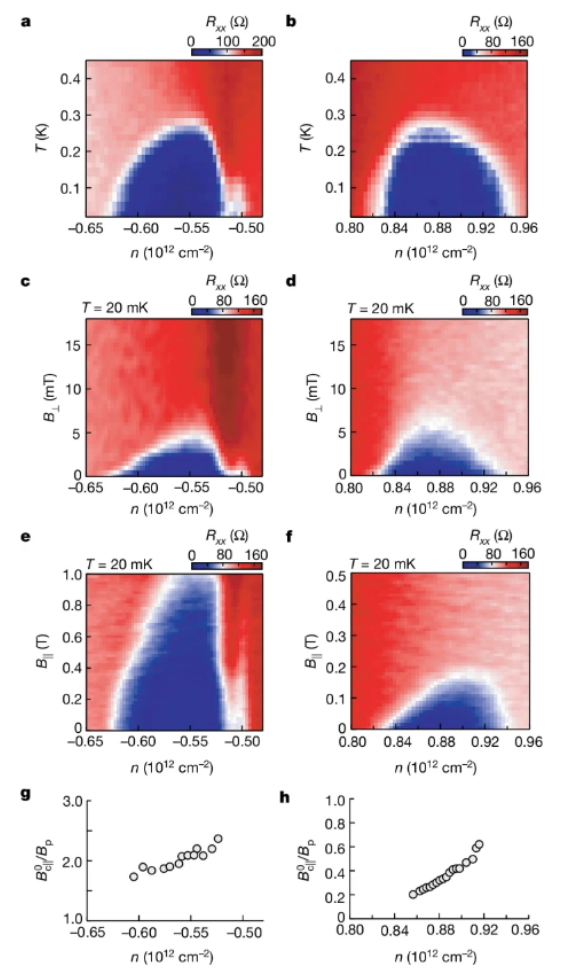
圖4. 空穴摻雜和電子摻雜超導電性的面內磁場依賴性。a,b,摻空穴超導圓頂(a)和摻電子超導圓頂(b)分別在 D = 0.96 V nm
-1 和 D = -1.64 V nm
-1 時 R
xx 與 T 和 n 的函數關系。c,d,摻空穴超導圓頂(c)和摻電子超導圓頂(d)分別在 D = 0.96 V nm
-1 和 D = -1.64 V nm
-1 時 R
xx 與 B
⊥ 和 n 的函數關系。e,f, R
xx 分別是 D = 0.96 V nm
-1 (e) 和 D = -1.64 V nm
-1 (f) 時 B∥ 和 n 的函數。在最佳摻雜條件下,空穴摻雜超導在 B∥ 高達 1 T 的條件下仍然可以存活,而在 D = -1.64 V nm
-1 條件下,整個電子摻雜超導圓頂在 B∥ ≈ 0.2 T 的小條件下被完全抑制。g,h, Pauli不相容率B
0c||/B
p 分別為 D = 0.96 V nm
-1 (g) 和 D = -1.64 V nm
-1 (h)時的Pauli不相容率與 n 的關系。誤差帶在圓圈范圍內。摻空穴的超導違反了保利極限,而摻電子的超導則遵守了保利極限。此外B
0c||/B
p 在摻空穴和摻電子超導中都表現出與密度相關的行為。
相關研究成果由武漢大學Fengcheng Wu和上海交通大學Xiaoxue Liu、Tingxin Li等人2024年發表在Nature (鏈接:https://www.nature.com/articles/s41586-024-07584-w)上。原文:Tunable superconductivity in electron- and hole-doped Bernal bilayer graphene
轉自《石墨烯研究》公眾號







