在扭曲的石墨烯層中觀察到了各種涌現的相關電子現象。據報道,許多電子結構預測都在探索這一新領域,但很少有動量分辨電子結構測量來測試它們。我們使用角度分辨光電發射光譜研究了扭曲雙層、單層對雙層和雙雙層石墨烯(tDBG)的扭曲相關(1°<θ<8°)能帶結構。采用混合k·p模型對層間耦合進行了實驗與理論的直接比較。在扭曲角、堆疊幾何結構和背柵電壓之間發現了定量一致性,驗證了模型并揭示了扭曲石墨烯中的場致間隙。然而,對于θ=1.5±0.2°的tDBG,在接近魔角θ=1.3°的情況下,在費米能級附近發現了一個平坦帶,測量帶寬Ew=31±5meV。對平帶和下一個價帶之間的間隙的分析顯示,實驗(Δh=46±5meV)和理論(Δh=5meV)之間存在偏差,表明該區域的晶格弛豫。
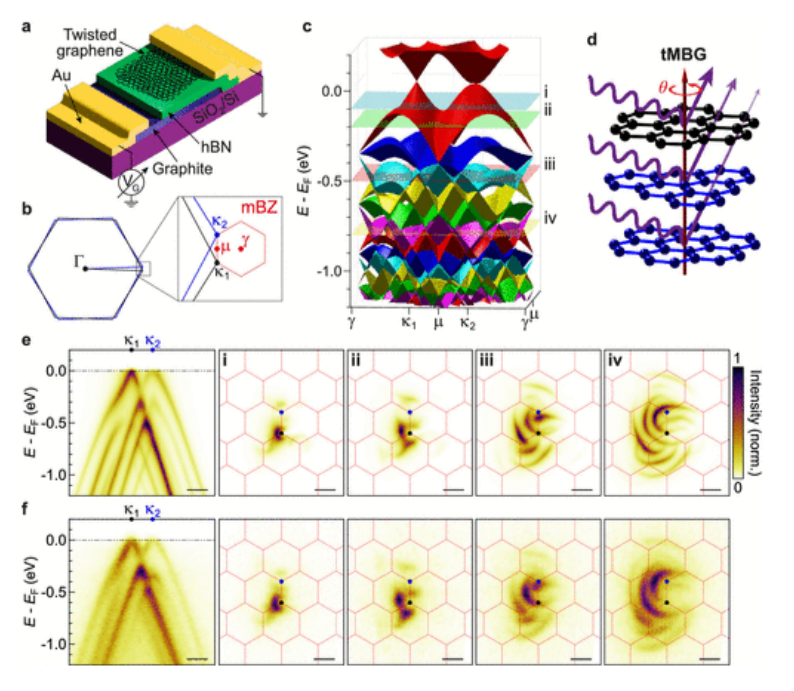
圖1.tMBG的模擬和測量ARPES光譜的比較。(a)扭曲的石墨烯異質結構和(b)扭曲石墨烯布里淵區和相應的莫爾布里淵區(mBZ)的示意圖。(c) 使用混合k·p模型計算θ=3.4°時tMBG的能帶結構。(d) 多層石墨烯的光電發射過程示意圖。來自較深層的光電子由于材料中的散射而衰減。(e) θ=3.4°時tMBG的模擬和(f)實驗ARPES光譜。左側面板顯示沿κ
1截取的能量-動量切割→ κ
2方向如b所示,其中κ
1對應于上層。面板i-iv是E–EF=(i)−100 meV、(ii)−200 meV、、(iii)−500 meV和(iv)−800 meV時的恒定能量圖,如(c)中的水平面所示。所有比例尺均為0.1Å
-1。
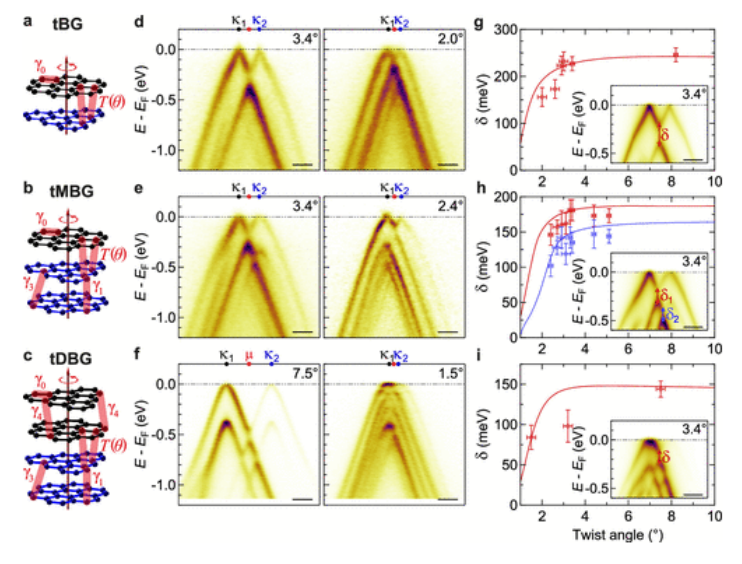
圖2:ARPES能量-動量譜的扭曲角和層數依賴性。(a–c)分別用層間和層內耦合參數標記的tBG、tMBG和tDBG的示意圖。(d–f)實驗ARPES能量動量在κ
1–κ
2方向上分別以2個扭轉角對tBG、tMBG和tDBG進行切割。(g–i)分別為tBG、tMBG和tDBG的雜交間隙大小與扭曲角的關系圖。實線對應于從模擬光譜中提取的數據,數據指向來自實驗光譜的數據。插圖顯示了相應層幾何結構在θ=3.4°時的模擬ARPES光譜,并標記了雜交間隙。所有比例尺均為0.1Å
-1。(e)中的第一個面板來自雙層石墨烯上的單層,第二個面板來自單層石墨烯上雙層。
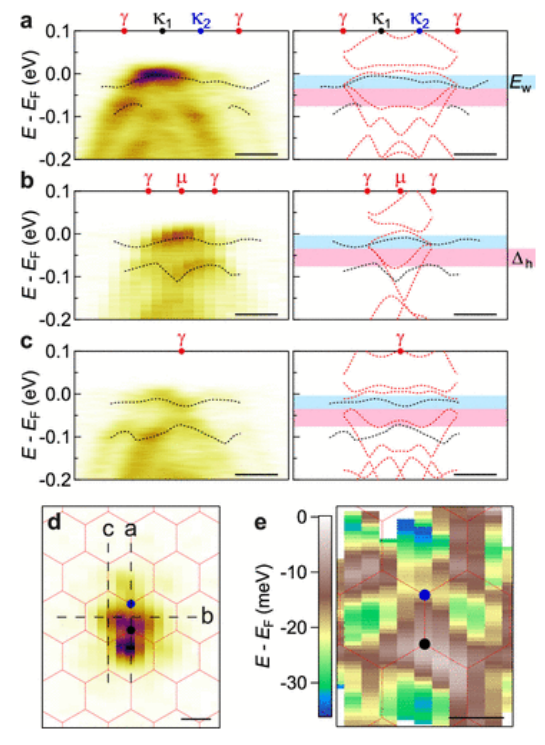
圖3.1.5°tDBG中的平帶色散。(a–c)能量-動量切割(左)沿著(d)中的黑色虛線和相應的能帶色散(右)。黑線對應于通過擬合EDC從實驗數據中提取的峰值位置,紅線對應于預測的電子結構。(d) 在E–E
F=−30 meV時的ARPES恒定能量圖,mBZs覆蓋在紅色中。(E)平坦帶的能量繪制在kx–ky平面上,mBZ覆蓋在紅色。所有比例尺均為0.05Å
-1。
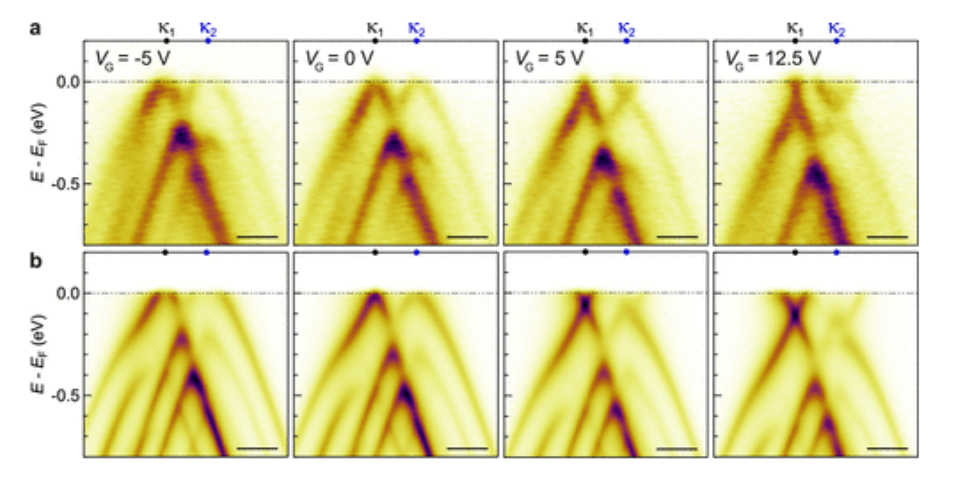
圖4. tMBG的靜電門控。(a)ARPES能量-動量切割3.4±0.1°tMBG,沿κ
1–κ
2方向在標記的柵極電壓下截取。(b)3.4°tMBG在不同背柵電壓下的模擬ARPES光譜,如圖所示。所有比例尺均為0.1Å
-1。
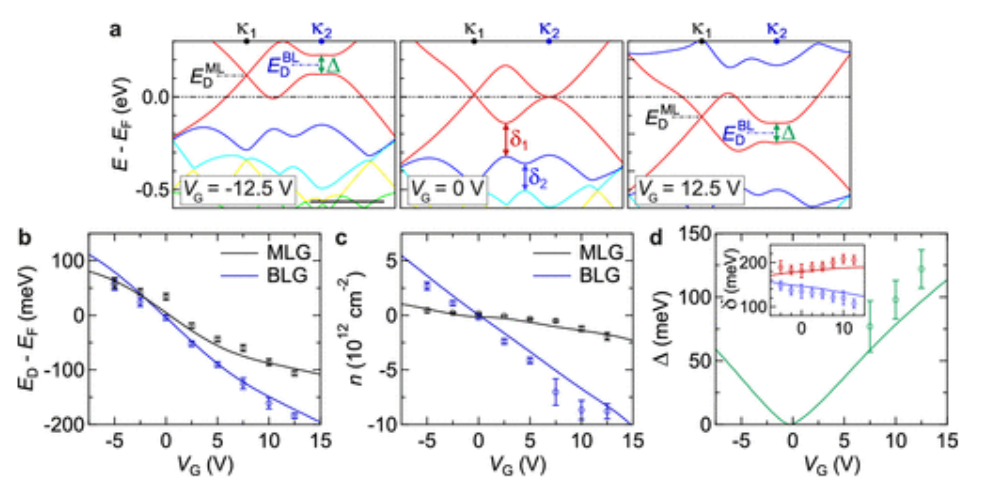
圖5. 在26nm hBN上3.4°tMBG的能帶結構變化和VG摻雜的分析。(a) tMBG在不同V
G下費米能級附近的能帶結構。標簽顯示了狄拉克點(E
D)、雙層間隙大小(Δ)和雜化間隙大小(δ)。比例尺為0.1Å-1。(b,c)對于單層(黑色)和雙層(藍色)狄拉克錐,狄拉克點能量E
D和載流子密度n分別作為V
G的函數。(d) 雙層狄拉克點的能隙Δ是V
G的函數。插圖顯示了作為V
G函數的雜交間隙,紅色的δ
1和藍色的δ
2。數據點是從ARPES數據中提取的實驗值,而實線是從模擬中提取的。
相關研究成果由曼徹斯特大學Roman V. Gorbachev和Vladimir I. Fal’ko,華威大學Neil R. Wilson 以及英國科學部Cephise Cacho 等人2023年發表在Nano Letter(https://doi.org/10.1021/acs.nanolett.3c01173)上。原文:ARPES Signatures of Few-Layer Twistronic Graphenes。
轉自《石墨烯研究》公眾號








