超薄石墨烯基膜已顯示出高性能納米機電(NEMS)器件的巨大前景。此類膜建模的關鍵挑戰在于,它們通常在不滿足“純彎曲”或“純拉伸”假設或近似值的偏轉狀態下運行。本研究基于Föppl–von Kármán(FvK)方程提出了石墨烯-聚合物異質結構(GPH)NEMS膜模型,該模型同時考慮了彎曲力和拉伸力。通過原子力顯微鏡形貌圖獲得的實驗GPH膜形狀與基于FvK的有限元方法模擬預測的膨脹形狀進行了比較,它們彼此之間顯示出極好的一致性。當在電容式壓力傳感器配置中GPH膜在壓力下偏轉時,通過準確預測偏轉GPH膜裝置在變化壓力下的電容變化,進一步證明了該模型的有效性。該模型在基于石墨烯的NEMS器件的設計和開發中是一個強大的新工具,能夠預測石墨烯NEMS器件性能或幫助設計器件幾何結構以匹配所需性能。
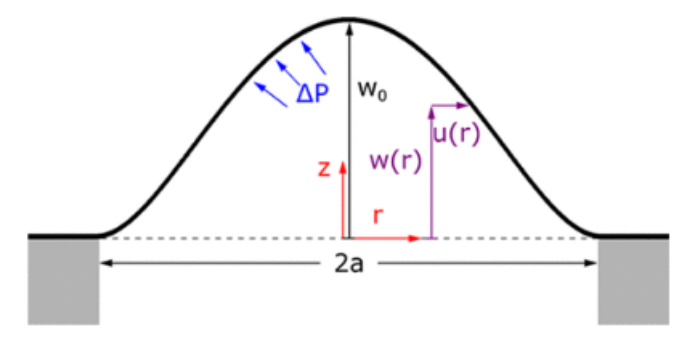
圖1.充氣軸對稱膜的橫截面示意圖和膜上的壓差。
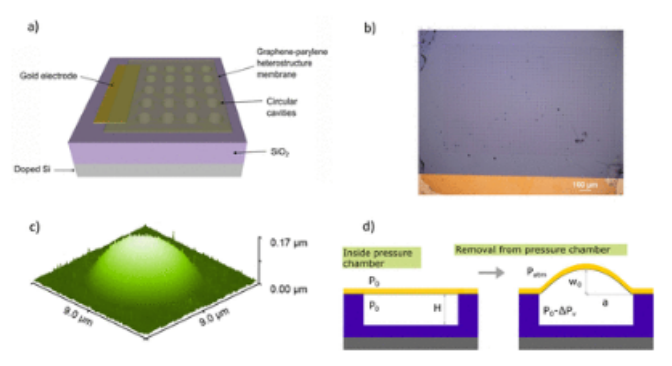
圖2. 傳感器設計和微泡膨脹測試。(a) GPH膜電容式壓力傳感器的3D示意圖。(b) 用于測量電容壓力響應的GPH膜電容壓力傳感器的光學顯微照片,包括金電極、GPH膜和空腔。(c) 膨脹泡罩的3D地形原子力顯微鏡(AFM)圖像,半徑a=3.5μm,厚度t=45 nm,壓力ΔP=0.94 kPa。(d)2D示意橫截面圖,描繪了具有單個空腔和致動膜的微泡膨脹測試程序,標記了重要參數。
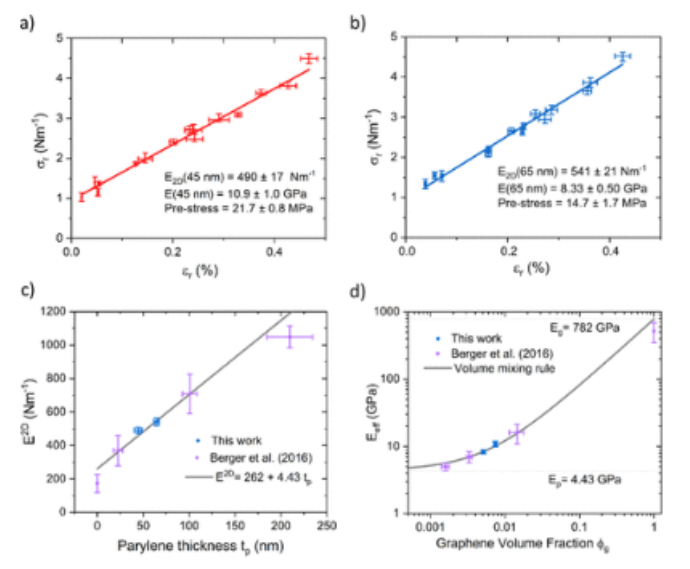
圖3. 微泡膨脹測試結果。(a,b)厚度為(a)45和(b)65 nm的GPH膜的徑向應力-應變圖,以及通過擬合從圖中提取的量(E、E
2D和預應力)。(c)測量E
2D與聚對二甲苯厚度,。對于本工作中的數據,y誤差條來自(a,b)的線性回歸中的不確定性。x誤差條是七個厚度測量值的標準偏差。(d)GPH膜的有效體積模量是石墨烯體積分數的函數,符合體積混合規則。兩條水平虛線表示提取的石墨烯和聚對二甲苯的體積模量。通過組合(a,b)的線性回歸中的誤差和膜厚度的不確定度來量化誤差條。Berger等人(2016)的數據誤差條通過結合所述E2D和膜厚度不確定度中的所述不確定度進行量化。
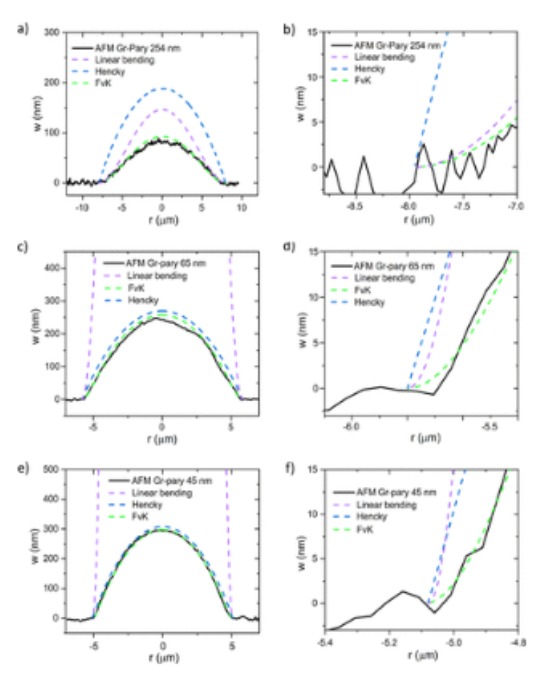
圖4. 與線性彎曲、Hencky解和FvK模型相比,GPH膜相對于徑向位置的偏轉。(a) 254 nm的膜厚加壓至ΔP=21 kPa。(b) 夾緊膜邊緣周圍(a)的放大。(c) 65 nm的厚度加壓至ΔP=68 kPa。(d) 夾緊膜邊緣周圍(b)的放大。(e) 加壓至ΔP=116 kPa的45 nm厚度。(f) 夾緊膜邊緣周圍(e)的放大。
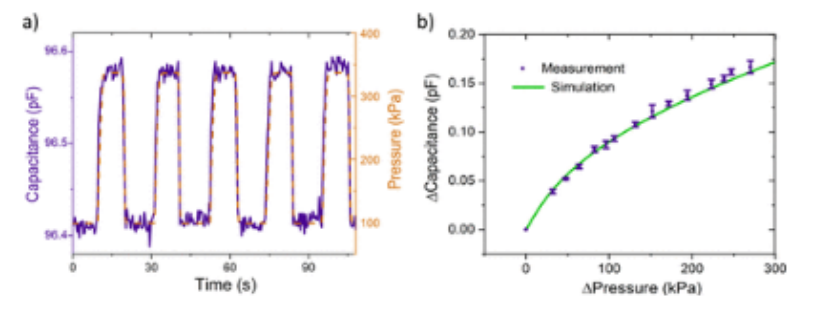
圖5. 電容–GPH電容式壓力傳感器的壓力響應。(a) 在340 kPa至大氣壓的五個壓力循環中,設備電容和外部壓力隨時間繪制。(b) 作為壓力變化函數的平均電容變化圖,將FvK FEM模擬與測量進行比較。誤差條是九個讀數的標準偏差。
相關研究成果由曼徹斯特大學Aravind Vijayaraghavan 等人2023年發表在ACS Applied Materials & Interfaces (https://doi.org/10.1021/acsami.2c21096)上。原文:Modeling Graphene–Polymer Heterostructure MEMS Membranes with the Föppl–von Kármán Equations。
轉自《石墨烯研究》公眾號








