在這項(xiàng)工作中,應(yīng)用三角剪切變形理論(TSDT)和Navier解方法,研究了碳納米管(CNT)增強(qiáng)夾層板在不同材料性能的不同堆疊順序下的靜態(tài)、自由振動(dòng)和相應(yīng)的模態(tài)振型。在TSDT中,位移沿板厚的分布是非線性的。在將所得結(jié)果與現(xiàn)有文獻(xiàn)中給出的結(jié)果進(jìn)行驗(yàn)證后,進(jìn)行了詳細(xì)的調(diào)查。對(duì)不同跨厚比、芯板厚度比、CNTs體積分?jǐn)?shù)和分布的功能梯度(FG) CNTs-增強(qiáng)夾層板的撓度、應(yīng)力、固有頻率和相應(yīng)的振型進(jìn)行了詳細(xì)的研究。
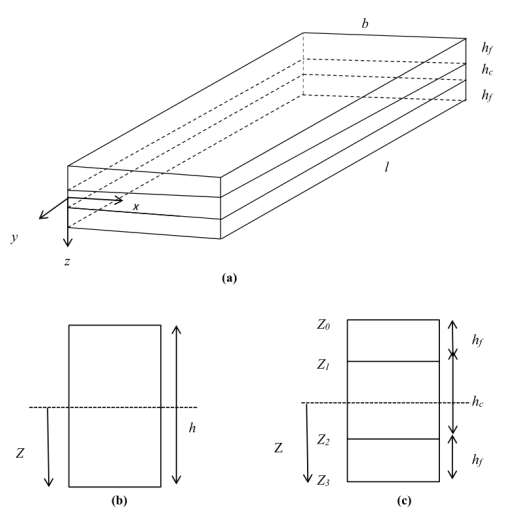
圖1.
a矩形板坐標(biāo)系x和y在平面方向和z軸沿厚度方向;
b矩形板橫截面;
c FG-CNTR夾層板,其中h
f為面板厚度,h
c為芯層厚度。
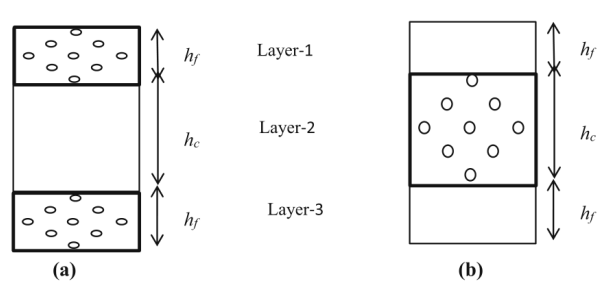
圖2.
aFG-CNTR夾層板的第1層和第3層為CNTs增強(qiáng)層,第2層為均質(zhì)層。
b 第1層和第3層為均質(zhì)層,第2層為CNTs-增強(qiáng)層。
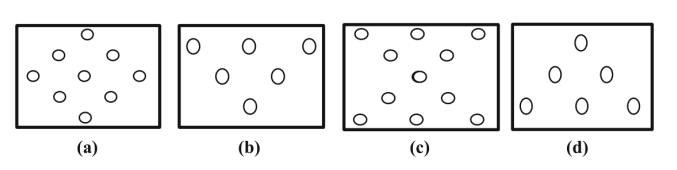
圖3.
a FG-O分布.
b FG-V分布.
c FG-X分布.
d FG-/\分布
.png)
圖4. 跨厚比隨橫向撓度變化的影響。
.png)
圖5. 軸向應(yīng)力σ
xx隨法向厚度變化的影響。
.png)
圖6. 前六階振型為自由振動(dòng)。
a 第一種模態(tài)(m=1,n=1);
b 第二種模態(tài)(m=1,n=2);
c 第三種模態(tài)(m=2,n=1);
d第四種模態(tài)(m=2,n=2);
e第五種模態(tài)(m=1,n=3);
f第六種模態(tài)(m=2,n=3)。
相關(guān)研究成果由貝拿勒斯大學(xué)土木工程系S. D. Singh等人于2021年發(fā)表在Archive of Applied Mechanics (https://doi.org/10.1007/s00419-021-01979-1)上。原文:Analytical solution for static and free vibration analysis of functionally graded CNT-reinforced sandwich plates。
轉(zhuǎn)自《石墨烯研究》公眾號(hào)
.jpg)




.png)
.png)
.png)
.jpg)


