超導電性和相關絕緣體在magic-angle twisted雙層石墨烯(MATBG)中的出現,提出了一種有趣的可能性,即其配對機制有別于傳統超導體,正如Bardeen-Coopero-Schrieffer (BCS)理論所描述的那樣,超導電性和相關絕緣體,在魔角雙層雙層石墨烯(MATBG)中的出現,提出了一種有趣的可能性,即其配對機制有別于傳統超導體。然而,最近的研究表明,即使庫侖相互作用被部分屏蔽,超導性仍然存在。這表明MATBG中的配對在本質上可能是傳統的,是其平坦帶的大的態密度(DOS)的結果。在這里,我們將隧道和Andreev反射光譜與掃描隧道顯微鏡(STM)相結合,在MATBG中觀察非常規超導的幾個關鍵實驗特征。結果表明,在過渡溫度T
c以下的隧穿譜與傳統的s波超導體的隧穿譜不一致,而與具有各向異性配對機制的節點超導體的隧穿譜相似。我們觀察隧道差距Δ
T之間存在很大差異,這遠遠超過了平均場BCS比率(2Δ
T / k
BT
c ~ 25),差距Δ
AR提取安德列夫反射光譜(2Δ
AR / k
BT
c ~ 6)。即使超導性被抑制,隧穿間隙仍然存在,這表明它是從偽間隙階段出現的。此外,當MATBG與六方氮化硼(hBN)排列時,贗隙和超導性均不存在。這些發現和本文報道的其他觀察結果為MATBG中超導的非BCS機制提供了優勢證據。
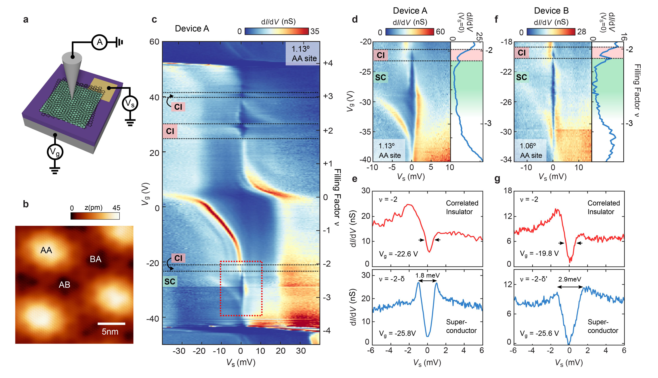
圖1 超導MATBG隧穿間隙的掃描隧穿光譜研究 a,實驗裝置原理圖。b, MATBG的STM地形圖像。c,在A器件AA位點拍攝的Tunneling dI/dV(Vs, Vg)顯示了固定在EF上的傳導和價平帶。d 器件A的高分辨率dI/dV(V
s, V
g)在ν =-2,和ν =-2與ν =-3之間的間隙。e 在Vg =-22.6 V和Vg =-25.8 V時,器件A的dI/dV(Vs)光譜。f,除B裝置(1.06,0.1%應變)外,與d相同。g在V
g =-19.8 V和V
g = -25.6 V時,器件B的dI/dV(Vs)光譜。
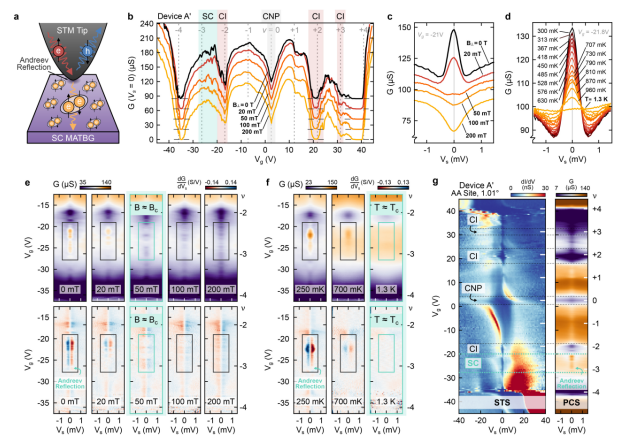
圖2 MATBG的點接觸光譜和Andreev反射 a利用密度調諧點接觸光譜(DT-PCS)測量安德烈耶夫反射過程的原理圖。b設備A在Vs = 0 V時接觸點G(V
g)的切線c在0 T和200 mT之間的五種磁場強度下,在Vg = -21 V超導載流子密度范圍內點接觸G(Vs)譜線切割。d,線切的點接觸型G (V
s)光譜, e在50 mT左右Andreev反射消失的面外磁場的不同值的點接觸G(Vs, Vg)和dG/ dVs(Vs, Vg)。在1.3 K左右Andreev反射消失的不同溫度值的點接觸G(Vs, Vg)和dG/dVs(Vs, Vg)。g將dI/dV(V
s, V
g)并排隧道到設備A中相同位置的AA位點和點接觸g (V
s, V
g)。
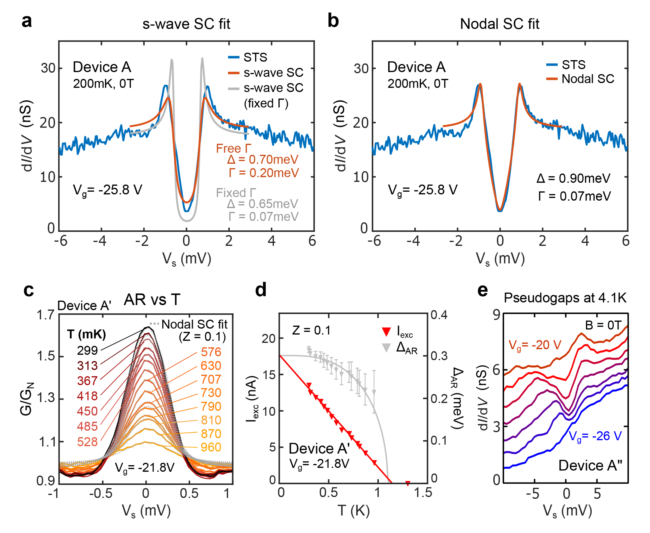
圖3 隧道和Andreev反射譜曲線擬合 a dyns -function與Vg = -25.8 V時的實驗隧穿光譜吻合b,除了對節點超導體與a相同, c,在300 mK和1 K之間的15個溫度下,在Vg = -21.8 V下,A '器件的Andreev反射光譜(實體曲線)與BTK模型(虛線曲線)相吻合d,從BTK中提取的過剩電流Iexc與超導能隙ΔAR吻合曲線。e A器件中在Vg = -20 V和Vg = -26 V之間的AA位點中心獲得的隧穿dI/dV(Vs)光譜。
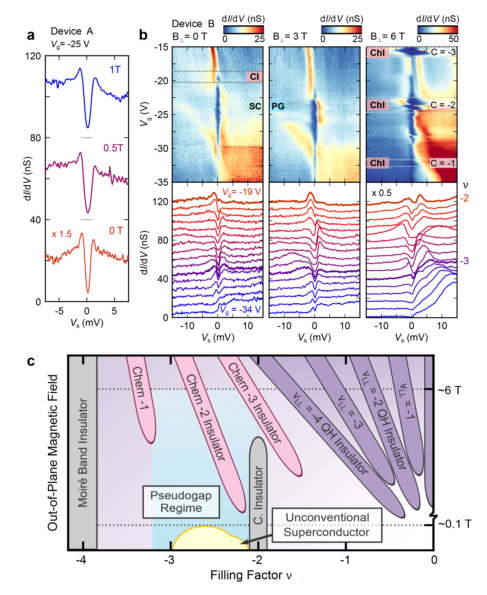
圖4. 空穴摻雜MATBG的贗隙狀態和相圖 a dI / dV,隧道(Vs)光譜Vg = -25 V帶的中心一個AA位點在B = 0 T,0.5T,和1 T,顯示突出的差距在EF的持久性遠高于MATBG. b,對于Vg = -19 V到Vg = -34 V,以及對于b = 0 T, 3 T,和6 T,在b器件AA位點上的隧道dI/dV(Vs, Vg)和dI/dV(Vs)光譜,清晰度曲線偏移7.5 nS。c,在空穴摻雜區域,MATBG作為平帶填充因子ν和磁場B的函數的相位示意圖。
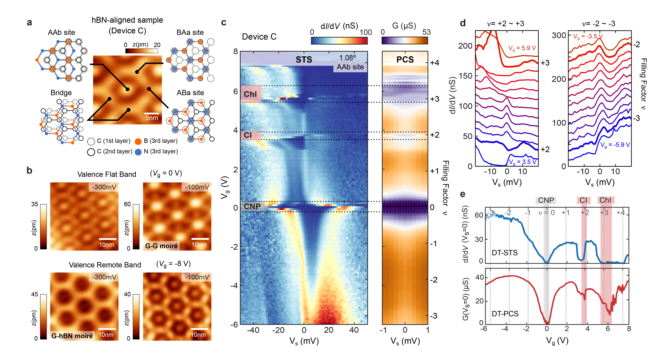
圖5 DT-STS和DT-PCS在非超導MATBG上對準hBN a,與底層hBN基底完全相稱的MATBG的STM圖像。b,不同Vs和Vg值的MATBG與hBN對齊的STM圖像, c,將dI/dV(Vs, Vg)引入AAb位點和G(Vs, Vg)的點接觸。d,來自c的dI/dV(Vs)光譜,清晰度偏移15 nS(左)和20 nS(右)。e,隧道dI/dV(Vg)和PCS G(Vg)線切割從c為Vs = 0 V。
相關科研成果由美國普林斯頓大學Ali Yazdani等人于2021年發表在Nature(https://doi.org/10.1038/s41586-021-04121-x)上。原文:Evidence for unconventional
superconductivity in twisted bilayer graphene。
轉自《石墨烯研究》公眾號
.jpg)

 圖1 超導MATBG隧穿間隙的掃描隧穿光譜研究 a,實驗裝置原理圖。b, MATBG的STM地形圖像。c,在A器件AA位點拍攝的Tunneling dI/dV(Vs, Vg)顯示了固定在EF上的傳導和價平帶。d 器件A的高分辨率dI/dV(Vs, Vg)在ν =-2,和ν =-2與ν =-3之間的間隙。e 在Vg =-22.6 V和Vg =-25.8 V時,器件A的dI/dV(Vs)光譜。f,除B裝置(1.06,0.1%應變)外,與d相同。g在Vg =-19.8 V和Vg = -25.6 V時,器件B的dI/dV(Vs)光譜。
圖1 超導MATBG隧穿間隙的掃描隧穿光譜研究 a,實驗裝置原理圖。b, MATBG的STM地形圖像。c,在A器件AA位點拍攝的Tunneling dI/dV(Vs, Vg)顯示了固定在EF上的傳導和價平帶。d 器件A的高分辨率dI/dV(Vs, Vg)在ν =-2,和ν =-2與ν =-3之間的間隙。e 在Vg =-22.6 V和Vg =-25.8 V時,器件A的dI/dV(Vs)光譜。f,除B裝置(1.06,0.1%應變)外,與d相同。g在Vg =-19.8 V和Vg = -25.6 V時,器件B的dI/dV(Vs)光譜。 圖2 MATBG的點接觸光譜和Andreev反射 a利用密度調諧點接觸光譜(DT-PCS)測量安德烈耶夫反射過程的原理圖。b設備A在Vs = 0 V時接觸點G(Vg)的切線c在0 T和200 mT之間的五種磁場強度下,在Vg = -21 V超導載流子密度范圍內點接觸G(Vs)譜線切割。d,線切的點接觸型G (Vs)光譜, e在50 mT左右Andreev反射消失的面外磁場的不同值的點接觸G(Vs, Vg)和dG/ dVs(Vs, Vg)。在1.3 K左右Andreev反射消失的不同溫度值的點接觸G(Vs, Vg)和dG/dVs(Vs, Vg)。g將dI/dV(Vs, Vg)并排隧道到設備A中相同位置的AA位點和點接觸g (Vs, Vg)。
圖2 MATBG的點接觸光譜和Andreev反射 a利用密度調諧點接觸光譜(DT-PCS)測量安德烈耶夫反射過程的原理圖。b設備A在Vs = 0 V時接觸點G(Vg)的切線c在0 T和200 mT之間的五種磁場強度下,在Vg = -21 V超導載流子密度范圍內點接觸G(Vs)譜線切割。d,線切的點接觸型G (Vs)光譜, e在50 mT左右Andreev反射消失的面外磁場的不同值的點接觸G(Vs, Vg)和dG/ dVs(Vs, Vg)。在1.3 K左右Andreev反射消失的不同溫度值的點接觸G(Vs, Vg)和dG/dVs(Vs, Vg)。g將dI/dV(Vs, Vg)并排隧道到設備A中相同位置的AA位點和點接觸g (Vs, Vg)。

 圖5 DT-STS和DT-PCS在非超導MATBG上對準hBN a,與底層hBN基底完全相稱的MATBG的STM圖像。b,不同Vs和Vg值的MATBG與hBN對齊的STM圖像, c,將dI/dV(Vs, Vg)引入AAb位點和G(Vs, Vg)的點接觸。d,來自c的dI/dV(Vs)光譜,清晰度偏移15 nS(左)和20 nS(右)。e,隧道dI/dV(Vg)和PCS G(Vg)線切割從c為Vs = 0 V。
圖5 DT-STS和DT-PCS在非超導MATBG上對準hBN a,與底層hBN基底完全相稱的MATBG的STM圖像。b,不同Vs和Vg值的MATBG與hBN對齊的STM圖像, c,將dI/dV(Vs, Vg)引入AAb位點和G(Vs, Vg)的點接觸。d,來自c的dI/dV(Vs)光譜,清晰度偏移15 nS(左)和20 nS(右)。e,隧道dI/dV(Vg)和PCS G(Vg)線切割從c為Vs = 0 V。.jpg)


